Resolución de un problema de regresión mediante una pequeña red neuronal con TensorFlow y PyTorch.
Introducción:
El avance de la inteligencia artificial y el aprendizaje automático ha revolucionado la forma en que abordamos diversos problemas en la actualidad. Entre las áreas más relevantes se encuentra el campo de la regresión, donde se busca predecir valores continuos en función de variables de entrada. En este proyecto, nos enfocaremos en la implementación de una pequeña red neuronal utilizando dos de las bibliotecas más populares y potentes en el ámbito del aprendizaje automático: TensorFlow y PyTorch.
El objetivo principal de este proyecto es resolver un problema de regresión específico utilizando ambas bibliotecas, comparar sus enfoques y obtener una visión más profunda de las particularidades de cada una. Para ello, seleccionaremos un conjunto de datos adecuado para el problema y lo prepararemos para el entrenamiento y evaluación de nuestros modelos.
El problema
El problema que queremos resolver es la conversión de metros a pies. La tarea consiste en construir un modelo de regresión que tome una medida en metros como entrada y prediga su equivalente en pies como salida.
La conversión entre estas dos unidades de longitud es una operación matemática relativamente sencilla, pero la utilizamos como un ejemplo para aprender y practicar el uso de TensorFlow en un problema de regresión. Aunque la conversión entre metros y pies se puede hacer de manera precisa mediante una simple multiplicación y división, este proyecto nos permitirá explorar los fundamentos del aprendizaje automático y cómo resolver problemas de regresión utilizando esta poderosa biblioteca.
Nuestro conjunto de datos de entrenamiento consistirá en pares de valores que representan medidas en metros y su equivalente en pies. Con estos datos, entrenaremos nuestro modelo de regresión para que aprenda la relación entre ambas unidades y pueda realizar conversiones precisas para nuevas medidas en metros.
TensorFlow
TensorFlow, desarrollado por el equipo de Google Brain, es una de las bibliotecas de código abierto más populares y poderosas en el campo del aprendizaje automático y la inteligencia artificial. Su nombre proviene de “tensor”, que se refiere a una estructura matemática multidimensional, fundamental para el procesamiento de datos en el aprendizaje profundo.
Lanzado en noviembre de 2015, TensorFlow se ha convertido en una herramienta esencial para científicos de datos, ingenieros y desarrolladores que buscan construir y entrenar modelos de aprendizaje automático de manera eficiente. Su enfoque flexible y versátil lo hace adecuado para una amplia gama de tareas, desde la clasificación y detección de objetos hasta el procesamiento del lenguaje natural y la regresión.
La fortaleza principal de TensorFlow radica en su capacidad para crear redes neuronales complejas mediante el uso de gráficos computacionales. Estos gráficos representan el flujo de datos y las operaciones matemáticas que ocurren en el proceso de entrenamiento del modelo. Además, TensorFlow ofrece la ventaja de poder aprovechar el poder de cómputo de GPU y TPU (Tensor Processing Unit), lo que acelera significativamente el proceso de entrenamiento y permite el manejo de grandes conjuntos de datos.
Otro aspecto destacado de TensorFlow es su naturaleza de código abierto, lo que ha llevado a una amplia comunidad de desarrolladores a contribuir con mejoras, extensiones y herramientas adicionales. La documentación detallada y numerosos recursos disponibles hacen que el aprendizaje de TensorFlow sea accesible para aquellos que deseen adentrarse en el mundo del aprendizaje automático.
Nuestro ejercicio :)
En este ejercicio, comenzaremos importando las librerías necesarias y definiendo nuestros datos de entrenamiento. En esta ocasión, utilizaremos un conjunto reducido de solo 7 datos. Cada dato consta de dos valores: el valor en metros y su equivalente en pies.
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
m = np.array([1, 8, 4, 5, 12, 10, 17], dtype=float)
pie = np.array([3.28084, 26.24672, 13.12336, 16.4042, 39.37008, 32.8084, 55.77428], dtype=float)
Luego procederemos a la creación del modelo, que constará de una única neurona de entrada y otra de salida. Esta estructura es sencilla pero efectiva para resolver nuestro problema de conversión de metros a pies. A pesar de su simplicidad, esta configuración nos permitirá obtener resultados precisos y eficientes para la tarea en cuestión.
capa = tf.keras.layers.Dense(units=1, input_shape=[1])
model = tf.keras.Sequential([capa])
Luego pasamos a compila el modelo para la tarea de regresión. El error cuadrático medio (mean_squared_error) se utiliza como función de pérdida y el optimizador ‘adam’ se elige para ajustar los pesos de la red durante el entrenamiento.
model.compile(loss='mean_squared_error',
optimizer='adam')
Con el modelo compilado, es momento de iniciar el entrenamiento con la tenacidad de un guerrero saiyajin.
historial = model.fit(m, pie, epochs=100, verbose = False)
Con la tarea hecha es hora de vizualizar nuestro resultados.
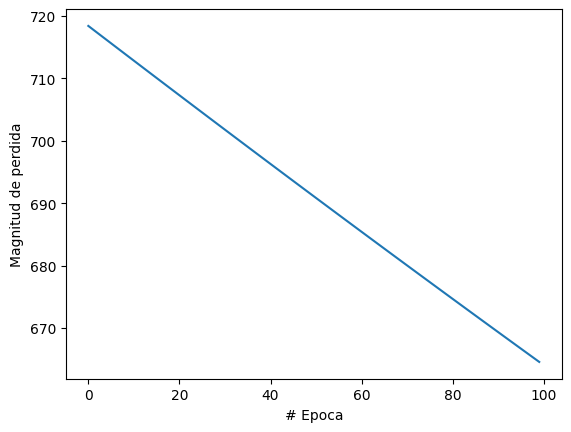
Dios mio!! como es posible este suceso!!. los resultados son malos pero igual vere la predicion que hace.
pies = model.predict([100])
print('El quivalente en pies es' + str(pies) )
1/1 [==============================] - 0s 41ms/step
El quivalente en pies es[[57.586525]]
No funciono? pipipipi aqui con mas epocas, otra cosa.
pies = model.predict([100])
print('El quivalente en pies es' + str(pies) )
1/1 [==============================] - 0s 41ms/step
El quivalente en pies es[[309.80557]]
Usaremos una grilla para encontrar intetar mejorar nuestro hiperparamentro y opteneer mejores resultados.
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras.wrappers.scikit_learn import KerasRegressor
from sklearn.model_selection import GridSearchCV
def create_model(learning_rate=0.01):
capa = tf.keras.layers.Dense(units=1, input_shape=[1])
model = tf.keras.Sequential([capa])
optimizer = tf.keras.optimizers.Adam(learning_rate=learning_rate)
model.compile(loss='mean_squared_error', optimizer=optimizer)
return model
m = np.array([1, 8, 4, 5, 12, 10, 17], dtype=float)
pie = np.array([3.28084, 26.24672, 13.12336, 16.4042, 39.37008, 32.8084, 55.77428], dtype=float)
# Crear el modelo para usarlo con GridSearchCV
model = KerasRegressor(build_fn=create_model, epochs=500, batch_size=1, verbose=0)
# Define los posibles valores para la tasa de aprendizaje (learning_rate)
param_grid = {'learning_rate': [0.001, 0.01, 0.1, 0.2, 0.25 , 0.3]}
# Realiza la búsqueda en cuadrícula
grid = GridSearchCV(estimator=model, param_grid=param_grid, scoring='neg_mean_squared_error', cv=3)
grid_result = grid.fit(m, pie)
# Muestra los resultados de la búsqueda
print("Mejor: %f usando %s" % (grid_result.best_score_, grid_result.best_params_))
# Entrena el modelo final con los mejores hiperparámetros encontrados
best_learning_rate = grid_result.best_params_['learning_rate']
final_model = create_model(learning_rate=best_learning_rate)
historial = final_model.fit(m, pie, epochs=500, verbose=0)
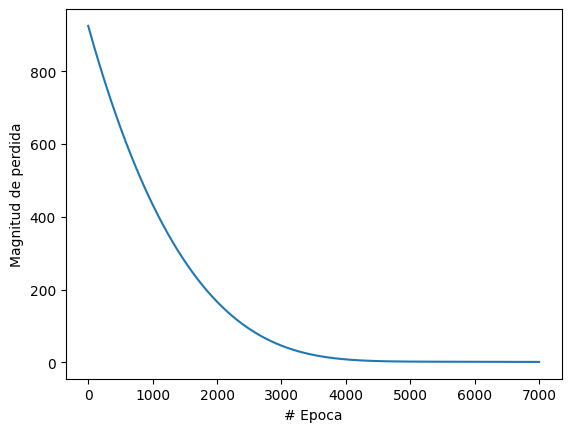
# Plot de la magnitud de la pérdida
plt.xlabel("# Epoca")
plt.ylabel("Magnitud de perdida")
plt.plot(historial.history["loss"])
plt.show()
El ganador fue: Mejor: -0.000000 usando {‘learning_rate’: 0.1}
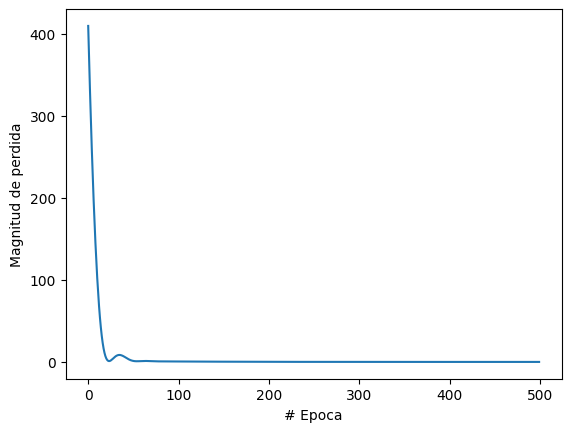
Nuestra prediccion resulto:
1/1 [==============================] - 0s 89ms/step
Predicción para m=100: [[327.94272]]
Bastante cerca de los 328.084 pies que equivalen 100m. :) Podemos notar que no seran necesario las 500 epocas podemos hacerla con unas 100, pero podemos configurar para que la red pare si es que no hay mejoras. Esto se hace con el “EarlyStopping”
early_stopping_callback = tf.keras.callbacks.EarlyStopping(monitor='loss', patience=7, min_delta=0.0001)
Esta línea de código crea una instancia del callback “EarlyStopping” proporcionado por TensorFlow/Keras, que es utilizado para implementar la técnica de detención temprana durante el entrenamiento del modelo.
-
monitor: El argumento ‘monitor’ especifica la métrica que el callback debe monitorear para determinar si se producen mejoras en el rendimiento del modelo. En este caso, estamos monitoreando la función de pérdida, que se define como ‘loss’ en el modelo. El callback “EarlyStopping” evaluará si la pérdida mejora o no en cada época para tomar decisiones sobre detener el entrenamiento.
-
patience: El argumento ‘patience’ representa el número de épocas que el callback esperará sin ver una mejora en la métrica especificada en ‘monitor’ antes de detener el entrenamiento. En este caso, hemos establecido patience=7, lo que significa que el entrenamiento se detendrá si no se observa mejora en la pérdida durante 7 épocas consecutivas.
-
min_delta: El argumento ‘min_delta’ es la cantidad mínima de cambio en la métrica que se considera como una mejora significativa. Si la diferencia entre dos épocas sucesivas de la métrica monitoreada es menor que ‘min_delta’, el callback no considerará que hay una mejora significativa. En este caso, hemos establecido min_delta=0.0001, lo que indica que cualquier mejora en la pérdida mayor que 0.0001 se considerará significativa.
Lo genial de esto es que nuestromodelo ya no entrena demas :)
PyTorch
La diferencia principal entre TensorFlow/Keras y PyTorch es la forma en que manejan el ciclo de entrenamiento. En Keras, puedes simplemente llamar al método fit en tu modelo, proporcionar tus datos de entrada y salida y especificar el número de épocas. Keras se encargará del resto. Sin embargo, en PyTorch, necesitas escribir tu propio ciclo de entrenamiento.
Este código de PyTorch crea una red neuronal de una sola capa, similar a la red Keras en tu pregunta. Luego entrena la red usando los datos proporcionados. Después de entrenar la red, la probamos con una entrada de 100 metros y la red devuelve la conversión a pies.
Por último, es importante señalar que los resultados de este modelo serán diferentes en cada ejecución debido a la inicialización aleatoria de los pesos de la red y a la naturaleza estocástica del optimizador Adam.
import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
m = np.array([1, 8, 4, 5, 12, 10, 17], dtype=float)
pie = np.array([3.28084, 26.24672, 13.12336, 16.4042, 39.37008, 32.8084, 55.77428], dtype=float)
m = torch.from_numpy(m).view(-1, 1).float()
pie = torch.from_numpy(pie).view(-1, 1).float()
class LinearModel(nn.Module):
def __init__(self):
super().__init__()
self.linear = nn.Linear(1, 1)
def forward(self, x):
return self.linear(x)
model = LinearModel()
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.1)
epochs = 100
losses = [] # Array to save the losses
for epoch in range(epochs):
model.train()
optimizer.zero_grad()
outputs = model(m)
loss = criterion(outputs, pie)
loss.backward()
optimizer.step()
losses.append(loss.item()) # Save the current loss
model.eval()
m_test = torch.Tensor([100]).view(-1, 1)
pies = model(m_test)
print('El equivalente en pies es ' + str(pies.item()))
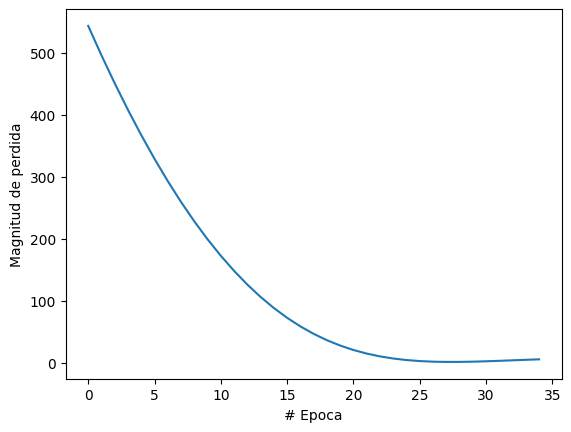
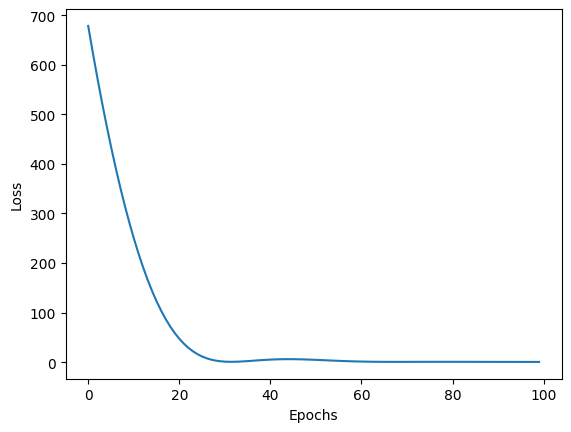
# Plotting the loss
plt.plot(range(epochs), losses)
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.show()
El equivalente en pies es 317.7523498535156
Para realizar una búsqueda de grilla, debes crear manualmente la grilla de parámetros que deseas explorar y luego iterar a través de esta grilla, entrenando y evaluando un modelo para cada combinación de parámetros
learning_rates = [0.1, 0.01, 0.001]
best_loss = float('inf')
best_lr = None
for lr in learning_rates:
model = LinearModel()
optimizer = torch.optim.Adam(model.parameters(), lr=lr)
for epoch in range(epochs):
model.train()
optimizer.zero_grad()
outputs = model(m)
loss = criterion(outputs, pie)
loss.backward()
optimizer.step()
if loss.item() < best_loss:
best_loss = loss.item()
best_lr = lr
print(f'Mejor tasa de aprendizaje: {best_lr}')
Para la parada temprana, debes monitorear alguna métrica de tu elección (generalmente la pérdida de validación) y dejar de entrenar si esta métrica deja de mejorar.
patience = 10
best_loss = float('inf')
epochs_no_improve = 0
for epoch in range(epochs):
model.train()
optimizer.zero_grad()
outputs = model(m)
loss = criterion(outputs, pie)
loss.backward()
optimizer.step()
if loss.item() < best_loss:
best_loss = loss.item()
epochs_no_improve = 0
else:
epochs_no_improve += 1
if epochs_no_improve == patience:
print(f'Parada temprana en la época {epoch}')
break

GITHUB
Se puede encontrar el notebook en mi github